A* pathfinding applied to roto poly edges
As I mentioned in my earlier posts about anti-aliasing, I'm currently working on a Nuke rotoscoping plugin. The default Nuke rotoscoping plugin is really an artist's drawing tool. You can define polys or paint on the image to create a roto matte. If you need a more precise edge, you'd usually use some sort of keying tool such as Ultimatte, Primatte, or Keylight. These tools are typically used with a green screen.
So, my little experiment: Coming from the games industry, I'm quite familiar with pathfinding algorithms. Would it be possible to use A* pathfinding (the simplest of them all) to refine a roto poly to follow the edge of an image, to give a result much closer to a chroma-keyed matte? This wouldn't work well for things like hair, but perhaps it might be useful in other situations.
Implementation
Here's the sample image that I'll be using initially for testing:

I expect this to be quite an "easy" image for this problem, since the edges are very clearly defined, but at least it's organic (the edges aren't straight), so we'll be able to see that the A* is doing its job. It's also not an ideal test case since this is the sort of image where you could easily get away with using a traditional rotoscoping tool, since a spline could follow those edges nearly perfectly. But it's often best to start with an easy case.
The first step to any A* pathfinding implementation is to create a heuristic to define the cost of moving from one node (or pixel in our case) to another adjacent pixel, typically in the 8 directions surrounding the pixel. So if we want to follow an edge, the "edgeness" of a pixel will be important, and it'll need to be part of our heuristic. An edge detection filter is the first step to deciding what is and isn't an edge.
I implemented a few of the most popular edge detection filters: Robert's Cross, Sobel, and Prewitt. I also tried a few variants of my own that I thought were quite clever. They weren't. The traditional methods always worked better.
Here, for example, is some code to implement Robert's Cross, the simplest edge filter:
void FilterImage::makeRobertsCross() {
foreach(z, channelMask) {
for (int iy = 0 ; iy < h - 1; ++iy) {
for (int ix = 0; ix < w - 1 ; ++ix) {
float v1 = m_tile[z][ y + iy ][ x + ix ];
float v2 = m_tile[z][ y + iy ][ x + ix + 1];
float v3 = m_tile[z][ y + iy + 1 ][ x + ix ];
float v4 = m_tile[z][ y + iy + 1 ][ x + ix + 1];
float v = std::abs(v1 - v4) + std::abs(v2 - v3);
m_data[ix + iy * w] += v;
}
}
}
}
I run the edge detection only on the portion of the image that requires it (as defined by where the user clicked the start and end points, with some buffer room around it to allow for backtracking). This gives me bright pixels where there's an edge. To make the A* follow the edge, I define a heuristic that says that the cost of moving from a pixel to another pixel is simply a function of the distance between the pixels (1, or 1.414 diagonally) times the 'non-edgeness' of the destination pixel. i.e. If it's not an edge, the value should be higher, and thus cost more to move there. So to assist in that calculation, I invert the edge filter after I calculate it, so that edges are dark (cheap) and non-edges are bright (expensive). I also do a bit of normalization of the image to make sure that the edges are a consistent value.
Here's what that looks like with a Sobel filter when applied to the whole image:
Let's try and walk the edge with the A* algorithm. Initial results seem promising as can be seen in this zoomed-in view:

At least we know we can successfully walk the edge, but this brings up a problem: I've written A-Buffer anti-aliasing code to render the generated edges, but these edges won't give smooth results at all. The edges lie between pixels when running horizontally and vertically, and only cross over a pixel when running diagonally. At best, our anti-aliasing is going to see three coverage values: 0, 1, or 0.5. It's going to look very pixelated.
I could shift the edge so that it lies on top of pixels instead of along their sides, but that's really only going to change the distribution and give you a lot of 0.5 coverage pixels that stair-step in an aliased fashion. We want something much better than that.
The edge needs to be smoothed to something less jagged. The first step is just to simplify it. It's currently composed of many 1 or 1.4 pixel length edges. The first thing we can do is run a pass over the path, looking for adjacent edges that point in the same direction and then merge them. This drastically reduces the number of edges and leads us to our next possible improvement.
At this point, we can draw upon a trick inspired by hardware anti-aliasing algorithms: When we see a short (< 1.5 pixel length) edge, remove it and replace it with the edge's centerpoint:
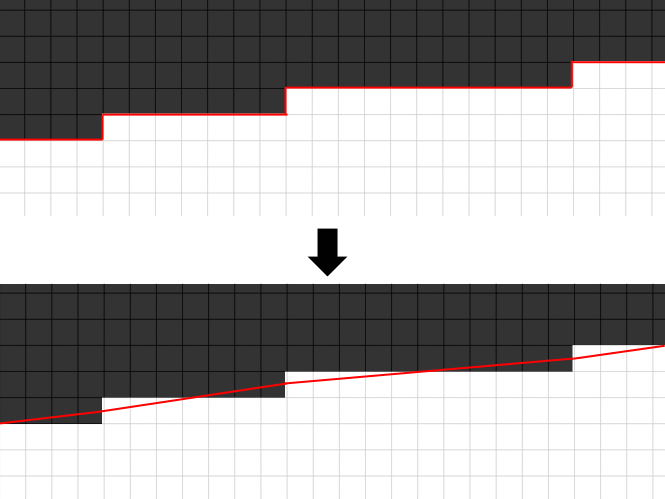
Let's see how that looks with our data:

That's starting to looks reasonable! We should see some high quality edges using this technique.